cs3003-unit1-notes

Insertion into Sorted List

Description

  1. It is assumed that there is a list A which has elements which are already sorted.

  2. The task at hand is to insert another element (referred to as key) into the sorted list A so that after the insertion, the list must continue to remain sorted.

  3. The key is made part of the sorted list by increasing the size by 1 and placing it as the last element of the list. Therefore, space complexity is O(1).

  4. An iteration of j is begun from i-1 all the way to 0

  • The key is compared with the last element A[j-1] of the sorted list. If the element is greater than the key, it is shifted right to A[j].

  1. If key is greater than the element in the list, insertion happens at the location j and the iteration is exited

  2. The function returns with the list containing key and maintaining the sort order.

Algorithm in pseudocode

func INSERT_INTO_SORTEDARRAY:
    (input) sorted list, and key to be inserted
    (output) sorted list with key inserted

    key: <- last element in A  // A is already sorted
    index: <- length(List) - 1

    iterate j from index to 1
        if A[j-1] > key then
            shift the element right
        else
            break

    if j != index:
        A[j] = key // inserted at the right location
    return A
end func

Example

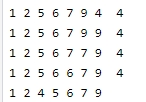
Assume sorted list ar = [3, 5, 6, 7] and element to insert is 2.

During the intermediary steps, the contents of ar are as shown below. The key is value 2 and eventually it gets inserted at beginning of the list.

Start: 3 4 6 7 2
    3 5 6 7 7  // 7 shifted right
    3 5 6 6 7  // 6 shifted right
    3 5 5 6 7  // 5 shifted right
    3 3 5 6 7  // 3 shifted right
    2 3 5 6 7  // 2 inserted in position 1 (index 0)
Final: 2 3 4 6 7

Source Code

def printarray(arr):
    for e in arr: print (e, end = " ")
    #print()

def insert_into_sortedArray(ar):
    key = ar[-1]  # the candidate to insert
    i = len(ar)-1 # position of candidate
    j = i

    while j > 0 and ar[j-1] > key:
        printarray(ar)
        print("", key)
        ar[j] = ar[j-1] # move bigger element right
        j = j-1
    if j != i:
        ar[j] = key
        printarray(ar)

Output

# sorted array
ar = [1, 2, 5,  6, 7, 9]
insert_into_sortedArray (ar + [4])

Tower of Hanoi

Pre-requisite: http://bit.ly/recursionELI5

The Tower of Hanoi problem is a popular puzzle that is used to introduce the concept of Recursion. It also helps to demonstrate the power of recursion in how it can present an elegation solution to a problem of medium complexity.

The rules one must follow when solving the tower puzzle are:

  1. Disks must be removed one at a time from the top of one tower and placed onto the top of another tower.

  2. No disk can be larger than any disk below it (i.e., the disks on each tower make a pyramid shape).

In our three-disc example, we had a simple base case of moving a single disc and a recursive case of moving all of the other discs (two in this case), using the third tower temporarily. We could break the recursive case into three steps:

1\.  Move the upper n-1 discs from tower A to B
    (the temporary tower), using C as the in-between.
2\.  Move the single lowest disc from A to C.
3\.  Move the n-1 discs from tower B to C,
    using A as the in-between.

The amazing thing is that this recursive algorithm works not only for three discs, but for any number of discs. We will codify it as a function called hanoi() that is responsible for moving discs from one tower to another, given a third temporary tower.

In our Towers of Hanoi solution, we recurse on the largest disk to be moved. That is, we will write a recursive function that takes as a parameter the disk that is the largest disk in the tower we want to move. Our function will also take three parameters indicating from which peg the tower should be moved (source), to which peg it should go (dest), and the other peg, which we can use temporarily to make this happen (spare).

Pseudocode 1

func moveDisk (A, B)
    print "Moving top disk from tower {A} to tower {B} "

func towerOfHanoi (n, fromTower, toTower, tempTower)
    if (n >= 1)
       towerOfHanoi(n-1, fromTower, tempTower, toTower)
       moveDisk(fromTower, toTower)
       towerOfHanoi(n-1, tempTower, toTower, fromTower)

end func

Pseudocode 2

Pseudo code:
BEGIN
    READ disk, source, dest, aux
    FUNCTION Hanoi (disk, source, dest, aux)
END

Pseudo code for function Hanoi (disk, source, dest, aux)
BEGIN
   IF disk=1 THEN
       Move disk from source to dest
   ELSE
       Hanoi (disk-1, source, aux, dest)
       Move disk from source to dest
       Hanoi (disk-1, source, aux, dest)
ENDIF
END

Output for 3 disc Hanoi Problem

Move top disk from tower Tower1 to tower Tower2
 Move top disk from tower Tower1 to tower Inter
 Move top disk from tower Tower2 to tower Inter
 Move top disk from tower Tower1 to tower Tower2
 Move top disk from tower Inter to tower Tower1
 Move top disk from tower Inter to tower Tower2
 Move top disk from tower Tower1 to tower Tower2

Python Code

Using http://bit.ly/hanoiInteractive

c = 0
def moveTower(height,fromPole, toPole, withPole):
    if height == 1:
        moveDisk(height, fromPole, toPole)
    else:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(height, fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)

def moveDisk(disk, fp,tp):
    global c
    c += 1
    print("Step", c, ": moving Disk", tower[disk], "from",fp,"to",tp)

tower = ['', 'red  ', 'green', 'blue ']
moveTower(3, "Start", "Dest", "Middle")

Hanoi Output

Step 1 : moving Disk red   from Start to Dest
Step 2 : moving Disk green from Start to Middle
Step 3 : moving Disk red   from Dest to Middle
Step 4 : moving Disk blue  from Start to Dest
Step 5 : moving Disk red   from Middle to Start
Step 6 : moving Disk green from Middle to Dest
Step 7 : moving Disk red   from Start to Dest

Thinking about Recursion

_Credits: http://bit.ly/recursionELI5

PreviousMergeSortNextcs3003-unit3

Last updated